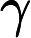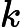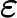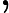El modelo AR de series temporales univariadas
Índice de contenido
Resumen:
En esta entrada, descubrirá el modelo AR: El modelo autorregresivo. El modelo AR (siglas de autoregressive) es el bloque de construcción más básico de series temporales univariadas. En este contexto, las series de tiempo univariadas son una familia de modelos que usan solo información sobre el pasado de la variable objetivo para pronosticar su futuro; por lo tanto, no se basan en otras variables explicativas.
¿Cómo citar el presente artículo?
Romero, J. (3 de febrero de 2018). El modelo AR de series temporales univariadas. Python.JeshuaRomeroGuadarrama. https://www.Python.jeshuaromeroguadarrama.com/es/blog/advanced-forecasting/the-ar-model-of-univariate-time-series/.
El modelo AR de series temporales univariadas by Jeshua Romero Guadarrama, available under Attribution 4.0 International (CC BY 4.0) at https://www.Python.jeshuaromeroguadarrama.com/es/blog/advanced-forecasting/the-ar-model-of-univariate-time-series/.
El modelo AR de series temporales univariadas
Introducción
En esta entrada, descubrirá el modelo AR: El modelo autorregresivo. El modelo AR (siglas de autoregressive) es el bloque de construcción más básico de series temporales univariadas. En este contexto, las series de tiempo univariadas son una familia de modelos que usan solo información sobre el pasado de la variable objetivo para pronosticar su futuro; por lo tanto, no se basan en otras variables explicativas.
Los modelos de series de tiempo univariantes pueden entenderse intuitivamente como bloques de construcción: Se suman desde el modelo más simple hasta modelos complejos que combinan los diferentes efectos descritos por modelos individuales. El modelo AR es el modelo más simple de los modelos de series temporales univariadas.
A lo largo de la siguiente entrada, se presentarán los componentes básicos de las series temporales univariadas. Así pues, el desarrollo de los conceptos partirá del modelo AR hasta el modelo SARIMA. Puede ver una descripción general esquemática de los bloques de construcción en series temporales univariadas en la Tabla 1.
Tabla 1. Los componentes básicos de las series de tiempo univariadas.
| Nombre | Explicación |
|---|---|
| AR | Autorregresivo |
| MA | Media móvil |
| ARMA | Combinación de modelos AR y MA |
| ARIMA | Agregar diferenciación (I) al modelo ARMA |
| SARIMA | Agregar estacionalidad (S) al modelo ARIMA |
| SARIMAX | Agregar variables externas (X) al modelo SARIMA (tenga en cuenta que las variables externas hacen que el modelo ya no sea univariante) |
Debo darte una alerta aquí, ya que el punto fuerte de este serie de entradas es brindar ejemplos de la vida real y realizar evaluaciones honestas y objetivas de diversos modelos. No puedo insistir lo suficiente en lo importante que resulta la evaluación del modelo, en vista de que el objetivo de cualquier modelo de pronóstico debe ser obtener el mejor rendimiento predictivo.
Dado que el modelo AR es el bloque de construcción más simple, sería poco realista esperar grandes rendimientos predictivos en la mayoría de los conjuntos de datos de la vida real. Aunque podría haber modificado el ejemplo para que encajara perfectamente o trabajar con un conjunto de datos simulado, prefiero mostrarle también las debilidades de ciertos modelos.
El modelo AR es excelente para comenzar a aprender sobre series temporales univariadas, pero es poco probable que use un modelo AR sin sus hermanos y hermanas en la práctica. Por lo general, trabajará con uno de los modelos combinados (SARIMA o SARIMAX) y probará cuáles son los componentes básicos que mejoran el rendimiento predictivo de su pronóstico.
Autocorrelación: El pasado influye en el presente
El modelo autorregresivo describe una relación entre el presente de una variable y su pasado. Por lo tanto, es adecuado para variables en las que los valores pasados y presentes se correlacionan.
Como ejemplo intuitivo, considere la línea de espera en el médico. Imagina que el médico tiene un plan en el que cada paciente tiene minutos con él. Si cada paciente tarda exactamente minutos, esto funciona bien. Pero, ¿y si un paciente tarda un poco más? Bueno, en estos casos existe una autocorrelación. La autocorrelación podría estar presente si la duración de una consulta tiene un impacto en la duración de la próxima consulta. Entonces, si el médico necesita acelerar una consulta porque la consulta anterior se demoró demasiado, se observará una correlación entre el pasado y el presente. En otras palabras, los valores pasados influyen en los valores futuros.
Calcular la autocorrelación en recuentos de terremotos
A lo largo de esta entrada, verá ejemplos aplicados al conocido conjunto de datos de terremotos. Este conjunto de datos es recopilado por el Centro Nacional de Información sobre Terremotos de EE. UU. Puede encontrar una copia del conjunto de datos en Kaggle.
Nota: Para obtener una descripción rápida de un conjunto de datos, se puede usar df.describe() para obtener estadísticas rápidas de cada columna en el marco de datos: recuento, media, desviación estándar, mínimo, máximo y cuantiles.
Para obtener una descripción más detallada, se puede utilizar el paquete de pandas que genera un reporte descriptivo de perfiles de forma automática:: profiling.
import warnings
warnings.filterwarnings('ignore')
# Instalar los paquetes necesarios con los siguientes comandos:
# !pip install pandas
# !pip install pandas-profiling
Si se importan los datos usando pandas, se puede recuperar una descripción del marco de datos usando el método describe, como se muestra en el siguiente código.
# Describiendo un marco de datos:
import pandas as pd
# Importar el marco de datos:
Terremotos = pd.read_csv('Terremotos.csv')
# Describir el marco de datos con el método df.describe():
Terremotos.describe().transpose()
| count | mean | std | min | 25% | 50% | 75% | max | |
|---|---|---|---|---|---|---|---|---|
| Latitude | 23412.0 | 1.679033 | 30.113183 | -77.080000 | -18.65300 | -3.5685 | 26.19075 | 86.005 |
| Longitude | 23412.0 | 39.639961 | 125.511959 | -179.997000 | -76.34975 | 103.9820 | 145.02625 | 179.998 |
| Depth | 23412.0 | 70.767911 | 122.651898 | -1.100000 | 14.52250 | 33.0000 | 54.00000 | 700.000 |
| Depth Error | 4461.0 | 4.993115 | 4.875184 | 0.000000 | 1.80000 | 3.5000 | 6.30000 | 91.295 |
| Depth Seismic Stations | 7097.0 | 275.364098 | 162.141631 | 0.000000 | 146.00000 | 255.0000 | 384.00000 | 934.000 |
| Magnitude | 23412.0 | 5.882531 | 0.423066 | 5.500000 | 5.60000 | 5.7000 | 6.00000 | 9.100 |
| Magnitude Error | 327.0 | 0.071820 | 0.051466 | 0.000000 | 0.04600 | 0.0590 | 0.07550 | 0.410 |
| Magnitude Seismic Stations | 2564.0 | 48.944618 | 62.943106 | 0.000000 | 10.00000 | 28.0000 | 66.00000 | 821.000 |
| Azimuthal Gap | 7299.0 | 44.163532 | 32.141486 | 0.000000 | 24.10000 | 36.0000 | 54.00000 | 360.000 |
| Horizontal Distance | 1604.0 | 3.992660 | 5.377262 | 0.004505 | 0.96875 | 2.3195 | 4.72450 | 37.874 |
| Horizontal Error | 1156.0 | 7.662759 | 10.430396 | 0.085000 | 5.30000 | 6.7000 | 8.10000 | 99.000 |
| Root Mean Square | 17352.0 | 1.022784 | 0.188545 | 0.000000 | 0.90000 | 1.0000 | 1.13000 | 3.440 |
Siéntase libre de desplazarse por la tabla descriptiva para comprender mejor de qué se tratan los datos.
Si desea una descripción más detallada de los datos, puede utilizar el paquete de pandas que genera un reporte descriptivo de perfiles de forma automática: profiling.
El resultado es una descripción muy detallada de las variables en el marco de datos. Puede usar el siguiente código para obtener un reporte de perfiles:
# Perfilando un marco de datos:
from pandas_profiling import ProfileReport
# Importar el marco de datos:
Terremotos = pd.read_csv('Terremotos.csv')
# Describir el marco de datos con el método df.profile_report():
# Terremotos.profile_report()
# Perfilando un marco de datos:
from pandas_profiling import ProfileReport
# Importar el marco de datos:
Terremotos = pd.read_csv('Terremotos.csv')
# Exportar el reporte de perfiles de pandas en formato html:
# reporte_perfiles = ProfileReport(Terremotos)
# reporte_perfiles.to_file(output_file = 'resultado.html')
Atención: El código anterior se ejecuta mejor en un Jupyter notebook o Jupyter lab (excelentes herramientas para el análisis exploratorio de datos). Ambos se pueden instalar directamente en su ordenador.
La alternativa a considerar es instalar Anaconda, que viene con muchas herramientas útiles de ciencia de datos y Python (la instalación incluye Jupyter notebook y Jupyter lab)
La tarea que se realizará es pronosticar la cantidad de terremotos fuertes por año. El conjunto de datos actualmente no tiene el formato correcto para hacer esto, ya que tiene una línea por terremoto y no una línea por año. Así pues, se deben preparar los datos para un análisis posterior; en consecuencia, se deben agregar los datos utilizando el siguiente código:
# Transformar la base de datos sobre terremotos a una base sobre la cantidad anual de terremotos:
import matplotlib.pyplot as plt
# Importar el marco de datos:
Terremotos = pd.read_csv('Terremotos.csv')
# Convertir años a fechas:
# Terremotos['año'] = pd.to_datetime(Terremotos['Date'], errors = 'coerce', format = '%m/%d/%Y').dt.year
Terremotos['Año'] = pd.to_datetime(Terremotos.Date, errors = 'coerce', format = '%m/%d/%Y').dt.year
# Filtrar la base de datos sobre terremotos a partir de una magnitud igual a 7 o superior:
# Terremotos = Terremotos[Terremotos['Magnitude'] >= 7]
Terremotos = Terremotos[Terremotos.Magnitude >= 7]
# Calcular un recuento de terremotos por año:
Terremotos_por_año = Terremotos.groupby('Año').count()
# Eliminar las otras variables de cada año:
Terremotos_por_año = Terremotos_por_año.iloc[1:-2, 0]
# Hacer una gráfica de terremotos por año:
ax = Terremotos_por_año.plot()
ax.set_ylabel('Número de terremotos')
ax.set_title('Evaluación del número de terremotos por año')
# Evaluación del número de terremotos por año:
plt.show()

El código anterior proporciona un gráfico que evalúa el número de sismos por año, mostrando que puede existir algún tipo de relación entre los años: Un año es más alto y un año es más bajo. Esto podría deberse a una autocorrelación negativa.
Resulta importante mencionar que una correlación negativa implica que un valor más alto en una variable corresponde a un valor más bajo en otra variable. Para la autocorrelación, esto significa que un valor más alto este año se corresponde con un valor más bajo el próximo año.
Ahora que se obtuvo la cantidad de terremotos por año, se debe verificar la autocorrelación numéricamente. En otras palabras, se debe averiguar si existe una correlación entre la cantidad de terremotos en un año determinado y el año anterior.
Para hacer esto, la correlación se puede calcular por pares, en dos columnas. No obstante, por ahora, solo se tiene una columna (los datos por año). Se deberá agregar una columna que contenga los datos de un año anterior. Esto se puede obtener aplicando un cambio a los datos originales y concatenando los datos cambiados con los datos originales. El siguiente código muestra cómo hacer esto:
# Graficar los datos desplazados:
cambios = pd.DataFrame(
{
'Este año': Terremotos_por_año,
'Año pasado': Terremotos_por_año.shift(1)
}
)
# Hacer una gráfica de los datos desplazados por año:
ax = cambios.plot()
ax.set_ylabel('Número de terremotos')
ax.set_title('Datos desplazados')
# Datos desplazados:
plt.show()

La figura previa muestra cómo los datos han cambiado año hacia atrás. Lo cual funciona bien, excepto por una cosa.
Como puede verse en los datos, existen observaciones desde hasta . Sin embargo, no se tiene un valor para el año de en la serie denominada Año pasado: En su lugar se introduce un valor nan (valor faltante, mejor conocido en la literatura como missing value).
Resulta importante mencionar que este tipo de efecto de borde es muy común en el análisis de series de tiempo. En estos casos, la mejor solución es dejar el año de fuera del análisis. Lo cual implica que debe eliminarse del marco de datos.
Se pueden eliminar todas las filas con datos faltantes usando el siguiente código:
# Eliminar datos faltantes:
cambios = cambios.dropna()
El siguiente paso es calcular el coeficiente de correlación de Pearson utilizando el código que se muestra a continuación (se omite la construcción del gráfico, dado que la matriz de correlación es más que suficiente):
# Calcular una matriz de correlación para el dataframe de cambios:
cambios.corr()
| Este año | Año pasado | |
|---|---|---|
| Este año | 1.000000 | 0.313667 |
| Año pasado | 0.313667 | 1.000000 |
En el siguiente párrafo, descubrirá cómo interpretar esta autocorrelación.
Autocorrelación positiva y negativa
Al igual que una correlación “regular”, la autocorrelación puede ser positiva o negativa. La autocorrelación positiva significa que un valor alto ahora probablemente dará un valor alto en el próximo período. Esto se puede observar, por ejemplo, en el comercio de acciones: Tan pronto como mucha gente quiere comprar una acción, su precio sube. Esta tendencia positiva hace que la gente quiera comprar esta acción aún más, ya que tiene resultados positivos. Cuanta más gente compra la acción, más sube y más gente querrá comprarla.
Una correlación positiva también funciona en las tendencias bajistas. Si el valor de las acciones de hoy es bajo, entonces es probable que el valor de mañana sea aún más bajo, ya que la gente comienza a vender. Cuando mucha gente vende, el valor cae, y aún más gente querrá vender. Este es también un caso de autocorrelación positiva, ya que el pasado y el presente van en la misma dirección:
- Si el pasado es bajo, el presente es bajo.
- Si el pasado es alto, el presente es alto.
De igual forma, existe autocorrelación negativa si dos tendencias son opuestas. Este es el caso en el ejemplo de la duración de la consulta del médico. Si una consulta lleva más tiempo, la siguiente será más corta. Si una consulta lleva menos tiempo, el médico puede tardar un poco más en la siguiente. Así pues, en el contexto de la autocorrelación negativa, se tiene que el pasado y el presente van en la dirección contraria:
- Si el pasado es bajo, el presente es alto.
- Si el pasado es alto, el presente es bajo.
En el código anterior, se puede observar una correlación de alrededor de entre el año actual y el año anterior. Esta correlación es positiva en lugar de negativa, como se esperaba según el gráfico. Dicha correlación es de fuerza media. Parece que la correlación ha capturado la tendencia en los datos. Si observa el gráfico, puede ver que hay una tendencia en el número de terremotos: Un poco más alto en los primeros años, luego un poco más bajo durante un cierto período y en los últimos años un poco más alto nuevamente. Esto es un problema, ya que la tendencia no es la relación que se desea capturar aquí.
Estacionariedad y la prueba ADF
El problema de tener una tendencia en los datos es general en el modelado de series temporales univariadas. La estacionariedad de una serie temporal significa que una serie temporal no tiene una tendencia (a largo plazo): Es estable alrededor del mismo promedio. De lo contrario, se dice que una serie de tiempo no es estacionaria.
En teoría, los modelos AR pueden tener un coeficiente de tendencia en el modelo, pero dado que la estacionariedad es un concepto importante en la teoría general de las series temporales, es mejor aprender a manejarlo de inmediato. Muchos modelos solo pueden funcionar en series de tiempo estacionarias.
Una serie de tiempo que está creciendo o disminuyendo fuertemente con el tiempo es obvia de detectar. Pero a veces es difícil saber si una serie de tiempo es estacionaria. Aquí es donde la prueba Augmented Dickey Fuller (ADF) resulta útil. La prueba de Dickey Fuller aumentada es una prueba de hipótesis que permite probar si una serie de tiempo es estacionaria. Se aplica como se muestra en el siguiente código:
from statsmodels.tsa.stattools import adfuller
# Prueba de Dickey Fuller Aumentada (ADF):
resultado = adfuller(Terremotos_por_año.dropna())
print("Resultado de la prueba de Dickey Fuller Aumentada (ADF):\n", resultado)
valor_p = resultado[1]
if valor_p < 0.05:
print('Estacionaria')
else:
print('No estacionaria')
Resultado de la prueba de Dickey Fuller Aumentada (ADF):
(-5.0088061338443275, 2.1319566272140453e-05, 0, 48, {'1%': -3.5745892596209488, '5%': -2.9239543084490744, '10%': -2.6000391840277777}, 202.7529751691226)
Estacionaria
En el caso de los datos sobre terremotos, se observa un valor p (p-value) menor que (el valor de referencia). Por ende, esto significa que la serie es teóricamente estacionaria: No se tiene que cambiar nada para aplicar el modelo AR.
Nota: Si no está familiarizado con las pruebas de hipótesis, debe saber que el valor p (p-value) es el valor concluyente para una prueba de hipótesis.
En una prueba de hipótesis, intenta probar una hipótesis alternativa frente a una hipótesis nula. El valor p (p-value) indica la probabilidad de que observe los datos que ha observado si la hipótesis nula fuera cierta. Si esta probabilidad es baja, concluye que la hipótesis nula debe ser incorrecta y, por lo tanto, la alternativa debe ser verdadera.
El valor de referencia para el valor p (p-value) es generalmente pero puede diferir para ciertas aplicaciones.
Diferenciar una serie de tiempo
Aunque la prueba ADF dice que los datos son estacionarios, se ha visto que la autocorrelación es positiva donde se esperaría que fuera negativa. La hipótesis era que esto podría ser causado por una tendencia.
Ahora tiene dos indicadores opuestos. Uno te dice que los datos son estacionarios y el otro te dice que hay una tendencia. Para estar seguro, es mejor eliminar la tendencia de todos modos. Esto se puede hacer mediante la diferenciación.
La diferenciación implica que, en lugar de modelar los valores originales de la serie temporal, se modelan las diferencias entre cada valor y el siguiente. Aunque haya una tendencia en los datos reales, probablemente no habrá una tendencia en los datos diferenciados. Para confirmar, puede volver a hacer una prueba ADF. Si aún no es bueno, puede volver a diferenciar la serie temporal diferenciada, hasta obtener un resultado correcto.
El siguiente código muestra cómo se pueden diferenciar fácilmente los datos en pandas:
import pandas as pd
# Diferenciar los datos:
datos_diferenciados = Terremotos_por_año.diff().dropna()
# Graficar los datos diferenciados:
ax = datos_diferenciados.plot()
ax.set_ylabel('Número diferenciado de terremotos')
# Datos diferenciados:
plt.show()

En el gráfico anterior se puede observar cómo se ven los datos diferenciados.
Ahora, para ver si esto ha cambiado la autocorrelación en la dirección correcta, se puede calcular el coeficiente de correlación como se hizo antes. El código para esto se puede observar a continuación. Adicional a la matriz de correlación, se pueden visualizar los datos desplazados y diferenciados en una gráfica:
# Autocorrelación de los datos diferenciados:
cambios_diferenciados = pd.DataFrame(
{
'Este año': datos_diferenciados,
'Año pasado': datos_diferenciados.shift(1)
}
)
ax = cambios_diferenciados.plot()
ax.set_ylabel('Número diferenciado de terremotos')
# Datos desplazados y diferenciados:
plt.show()
# Autocorrelación en datos diferenciados:
cambios_diferenciados.corr()

| Este año | Año pasado | |
|---|---|---|
| Este año | 1.000000 | -0.376859 |
| Año pasado | -0.376859 | 1.000000 |
La matriz de correlación muestra el coeficiente de correlación entre los datos diferenciados desplazados y los datos diferenciados no desplazados.
Ahora bien, se obtiene un coeficiente de correlación de , como se puede analizar en la matriz anterior: Se ha eliminado con éxito la tendencia de los datos. Su correlación es ahora la correlación negativa que se esperaba. Si hay más terremotos en un año, por lo general se tendrán menos terremotos el próximo año.
Retrasos en la autocorrelación
Además de la dirección de la autocorrelación, la noción de retraso (lag) es importante. Esta noción es aplicable solo en autocorrelación y no en correlación “regular”.
El número de retrasos (lags) de una autocorrelación significa el número de pasos hacia atrás en el tiempo que tienen un impacto en el valor presente. En muchos casos, si la autocorrelación está presente, no es solo el paso de tiempo anterior el que tiene un impacto, sino que pueden ser muchos pasos de tiempo.
Aplicado al ejemplo de la duración de la consulta del médico, podría imaginar que un médico tiene un retraso muy largo en una consulta y que necesita acelerar para las próximas tres consultas. Esto significaría que la tercera consulta “rápida” todavía está impactada por la retrasada. Entonces, el retraso de la autocorrelación sería al menos tres: Tres pasos atrás en el tiempo.
El ejemplo de duración de la consulta del médico es muy intuitivo, ya que es muy lógico que un médico tenga un tiempo limitado. En el ejemplo de los terremotos por año, no existe una lógica tan clara que explique las relaciones entre valores pasados y valores actuales. Esto hace que sea difícil identificar intuitivamente el número de retrasos que deben incluirse.
Una gran herramienta para investigar la autocorrelación en múltiples retrasos al mismo tiempo es usar el gráfico de autocorrelación del paquete statsmodels. ACF es la abreviatura de función de autocorrelación (autocorrelation function, por sus siglas en inglés): La autocorrelación en función del retraso. El código para gráficar la función de autocorrelación se muestra a continuación:
from statsmodels.graphics.tsaplots import plot_acf
import matplotlib.pyplot as plt
# Autocorrelación de los datos diferenciados:
plot_acf(datos_diferenciados, lags = 10)
# Gráfico de autocorrelación:
plt.show()

Se debe tener en cuenta que la elección de retrasos es arbitraria: Es solo para fines del graficado. Diez retrasos significan 10 años atrás en el tiempo, lo cual debería ser suficiente para mostrar autocorrelaciones relevantes, aunque o incluso más también sería una opción aceptable.
Se obtiene el gráfico previo. Dicho gráfico muestra qué autocorrelaciones es importante conservar. En el eje , verá el coeficiente de correlación entre los datos no retrasados (datos originales) y los datos retrasados. El coeficiente de correlación está entre y . En el eje se ve el número de retrasos (lags) aplicados, en este caso de a . La primera correlación es , ya que estos son los datos con retrasos: Los datos originales.
En este gráfico, se deben buscar valores de autocorrelación que sean al menos superiores a o inferiores a . Cualquier cosa por debajo de eso puede considerarse ruido. También es posible usar o como valor mínimo: No existe una guía estricta para interpretar el coeficiente de correlación, ya que en algunos dominios los datos son más ruidosos por naturaleza. Por ejemplo, en estudios sociales, cuando se trabaja con mediciones de estudios de cuestionarios, a menudo verá mucho más ruido que cuando se trabaja con mediciones físicas precisas.
El área azul del gráfico permite detectar visualmente qué autocorrelaciones son solo ruido: Si el pico sale del área azul, existe una autocorrelación significativa, pero si el pico permanece dentro del área azul, la autocorrelación observada es insignificante. En general, puede esperar que la autocorrelación sea mayor en los retrasos que están más cerca del presente y disminuya hacia los momentos más lejanos.
En el gráfico resultante de correr el código, se observa un primer pico (con retraso ), que es muy fuerte. Esto es normal, ya que son los datos originales. La correlación entre una variable y consigo misma es siempre (). El segundo pico es la correlación con retraso . Esta es la autocorrelación que ha calculado antes de usar la matriz de correlación. El coeficiente de correlación fue de , se puede ver nuevamente en este gráfico.
Las autocorrelaciones restantes son menos fuertes. Esto quiere decir que para saber el número de terremostos hoy, debemos fijarnos principalmente en los valores de un retraso; en el ejemplo actual, esto significa que debemos fijarnos en el número de terremotos durante el año pasado. Si hubo muchos terremotos el año pasado, podemos esperar menos terremotos este año: Esto lo indica la autocorrelación negativa para el retraso .
En aras de comprender cómo interpretar más retrasos, imagine una gráfica ACF diferente (hipotética) con solo un pico positivo en el retraso y los otros retrasos son todos . Esto significaría que para comprender la cantidad de terremotos de este año, se necesita mira lo que pasó hace años: Si hubo muchos terremotos hace cinco años, habrá muchos terremotos este año. Lo que sucedió en el medio no es relevante: Dado que no hay autocorrelación con los cuatro años anteriores, la cantidad de terremotos en los cuatro años anteriores no te ayudará a determinar la cantidad de terremotos este año. Esto podría ser, por ejemplo, un caso de estacionalidad durante períodos de años.
Autocorrelación parcial
El gráfico de autocorrelación parcial es otro gráfico que también debe observarse. La diferencia entre la autocorrelación y la autocorrelación parcial es que la autocorrelación parcial garantiza que ninguna correlación se cuente varias veces para múltiples retrasos. Por lo tanto, la autocorrelación parcial para cada retraso es una autocorrelación adicional a cada retraso inferior. En este sentido, es matemáticamente correcto decir que la autocorrelación parcial es una autocorrelación condicionada a retrasos anteriores.
Esto tiene un valor añadido, ya que las correlaciones en el gráfico de autocorrelación pueden ser redundantes entre sí.
La idea es más fácil de entender en un ejemplo hipotético. Imagine un caso hipotético en el que los valores para el presente, retraso y retraso , son exactamente iguales. Un gráfico de autocorrelación le diría que existe una autocorrelación perfecta tanto con el retraso como con el retraso . En constraste, el gráfico de autocorrelación parcial le diría que existe una autocorrelación perfecta con el retraso , pero no mostraría una autocorrelación para el retraso . Como siempre debe intentar hacer modelos con el menor número de variables necesarias (a menudo denominadas la navaja de Occam o el principio de parsimonia); en este sentido, sería mejor incluir solo el retraso y no el retraso .
PACF es la abreviatura de función de autocorrelación parcial (partial autocorrelation function, por sus siglas en inglés): La autocorrelación en función del retraso. Puede calcular la gráfica de autocorrelación parcial usando el paquete statsmodels, como se muestra en el siguiente código:
from statsmodels.graphics.tsaplots import plot_pacf
# Autocorrelación parcial de los datos diferenciados:
plot_pacf(datos_diferenciados, lags = 20)
# Autocorrelación parcial:
plt.show()

El código proporciona la gráfica que se muestra arriba. Como se puede ver, según el sombreado de fondo azul del gráfico, el PACF muestra el primer y el segundo retraso fuera del área sombreada. Esto significa que sería interesante incluir también el segundo retraso en el modelo AR.
¿Cuántos retrasos incluir?
Ahora, la gran pregunta en el análisis de series de tiempo es siempre cuántos retrasos incluir. Esto se llama el orden de la serie de tiempo. La notación es AR(1) para el orden 1 y AR(p) para un orden p.
El orden lo decides tú. Teóricamente hablando, puede fundamentar la elección del orden en el gráfico PACF. La teoría dice que se debe tomar el número de retrasos antes de obtener una autocorrelación de . Todos los demás retrasos deberían ser .
En la teoría, a menudo se ven grandes gráficos donde el primer pico es muy alto y el resto es igual a cero. En esos casos, la elección es fácil: Se está trabajando con un ejemplo muy “puro” de AR(1). Otro caso común es cuando su autocorrelación comienza alta y disminuye lentamente a cero. En este caso, debe usar todos los retrasos en los que el PACF aún no sea cero.
Sin embargo, en la práctica, no siempre es tan simple. Recuerda el famoso dicho “todos los modelos están mal, pero algunos son útiles”. Es muy raro encontrar casos que se ajusten perfectamente a un modelo AR. En general, el proceso de autorregresión puede ayudar a explicar parte de la variación de una variable, pero no toda.
En el ejemplo del terremoto, todavía existe un poco de autocorrelación parcial en retrasos posteriores, y esto continúa hasta retrasos muy lejanos. Incluso hay un pico de PACF en el retraso . Esto podría significar muchas cosas: Tal vez realmente haya una autocorrelación con retrasos lejanos o tal vez hay un proceso oculto subyacente que el modelo AR no está capturando bien.
En la práctica, se intentará seleccionar el número de retrasos que atribuyan al modelo el mejor rendimiento predictivo. El mejor rendimiento predictivo a menudo no se define mirando los gráficos de autocorrelación: Dichos gráficos brindan una estimación teórica, aunque el rendimiento predictivo se define mejor mediante la evaluación del modelo y la evaluación comparativa (más adelante se profundizará en cómo utilizar las técnicas de evaluación y elegir un orden de desempeño para el caso de los modelos AR). No obstante, antes de entrar en más detalles sobre la elección de un orden, es hora de profundizar en la definición exacta del modelo AR.
Definición del modelo AR
Hasta ahora, se han visto muchos aspectos del modelo autorregresivo de manera intuitiva. Como se vio antes, las autocorrelaciones muestran, para cada retraso, si existe una correlación con el presente. El modelo AR usa esas correlaciones para hacer un modelo predictivo.
Pero aún falta la parte más importante: La definición matemática del modelo AR. Para realizar una predicción basada en la autocorrelación, se deben expresar los valores futuros de la variable de destino como una función de las variables retrasadas. Para el modelo AR, esto da la siguiente definición de modelo:
En esta fórmula, es el valor actual y se calcula como la suma de cada valor retrasado multiplicado por un coeficiente para ese retraso en específico. El error al final es ruido aleatorio que no se puede predecir, pero sí se puede estimar.
Estimación del modelo AR usando las ecuaciones de Yule-Walker
Ya se ha visto la definición del modelo AR. En otros términos, se ha definido su forma. Sin embargo, no se puede usar mientras no se tengan los valores para ingresar a la fórmula. El siguiente paso es ajustar el modelo: Se necesitan encontrar los valores óptimos de cada coeficiente para poderlos emplear (a esto también se le conoce como estimar los coeficientes).
Una vez que se tienen los valores para los parámetros, es relativamente fácil usar el modelo: Simplemente se deben introducir los valores retrasados. Pero como en cualquier curso teórico de aprendizaje automático, la parte difícil siempre está en estimar el modelo.
En la fórmula, se puede apreciar que los valores pasados () se multiplican por un coeficiente (). La suma de esto da el valor actual . Al comenzar a ajustar el modelo, ya se conocen los valores pasados y el valor actual. Los únicos que no se conocen son los valores de (). Los son lo que se necesita encontrar matemáticamente para definir el modelo. Una vez que se estiman esos , se podrá calcular el valor de de mañana utilizando el estimado y los valores conocidos pasados y actuales.
Para el modelo AR se han encontrado diferentes métodos para estimar los coeficientes (los ), pero generalmente se acepta el método de Yule-Walker como el método más adecuado.
El método Yule-Walker
El método Yule-Walker consiste en un conjunto de ecuaciones:
En esta fórmula, es la función de autocovarianza de . Asimismo, es el número de retrasos de a ( es el retraso máximo). Por lo tanto, hay ecuaciones. De igual forma, es la desviación estándar de los errores.
Finalmente, es la función delta de Kronecker: Devuelve si ambos valores son iguales (si es igual a ) y si son diferentes ( no es ). En este contexto, se puede ver que esto significa que todo lo que sigue al signo es igual a si es y, en caso contrario, el todo es igual a . Por lo tanto, solo hay una ecuación después del signo que tiene esta parte, mientras que lo demás (de a ) no tiene dicha parte.
La clave para resolver esto es comenzar solo con las ecuaciones de a ( ecuaciones) escritas en formato matricial:

Esto se puede escribir en notación matricial como:
Para obtener los valores de , se puede utilizar el método de los Mínimos Cuadrados Ordinarios (OLS, por sus siglas en inglés: “Ordinary Least Squares”). El método de los mínimos cuadrados ordinarios es un cálculo matricial que se aplica ampliamente en estadística para resolver problemas como este. Permite estimar coeficientes en los casos en que se tiene una matriz con datos históricos y un vector con resultados históricos. La solución para encontrar las mejores estimaciones para el es la siguiente:
Una vez que se haya aplicado el método de OLS, se habrán obtenido las estimaciones de y, luego, se podrá calcular el utilizando el estimado para resolver:
Ahora bien, se comenzará a ajustar el modelo AR en Python, usando el código que se muestra a continuación. Ajustar el modelo, en este escenario, significa identificar los mejores valores posibles para el . Debe tenerse en cuenta que, como se está trabajando con datos reales y no con una muestra simulada, el trabajo consiste en lograr el mejor ajuste posible del modelo AR.
from statsmodels.regression.linear_model import yule_walker
# Estimar los coeficientes del modelo AR usando las ecuaciones de Yule-Walker con orden 3:
coeficientes, sigma = yule_walker(datos_diferenciados, order = 3)
print('Coeficientes: ', -coeficientes)
print('Sigma: ', sigma)
Coeficientes: [0.51636104 0.34981679 0.08922855]
Sigma: 3.99051873543974
Los coeficientes obtenidos con este método son los coeficientes para cada una de las variables rezagadas. En este caso, el orden es 3, por lo que debe aplicarse a los tres últimos valores para calcular el nuevo valor. Puede hacer un pronóstico calculando los próximos pasos, en función de los coeficientes actuales. El código para esto se muestra a continuación:
from statsmodels.regression.linear_model import yule_walker
# Realizar un pronóstico con los coeficientes estimados del modelo AR:
coeficientes, sigma = yule_walker(datos_diferenciados, order = 3)
# Hacer una lista de valores diferenciados:
lista_valores = list(datos_diferenciados)
# Invertir la lista para que el orden corresponda con el orden de los coeficientes:
lista_valores.reverse()
# Definir el número de años para predecir:
numero_pasos = 10
Atención: Cuantos más pasos adelante se deseen pronosticar, más difícil se vuelve (es probable que el error aumente con la cantidad de pasos).
# Predecir para cada año:
for i in range(numero_pasos):
# Calcular el nuevo valor como:
# La suma de los valores rezagados.
# Multiplicada por el coeficiente correspondiente.
nuevo_valor = 0
for j in range(len(coeficientes)):
nuevo_valor += coeficientes[j] * lista_valores[j]
# Insertar el nuevo valor al principio de la lista:
lista_valores.insert(0, nuevo_valor)
# Rehacer la lista de valores al revés para mantener el orden del tiempo:
lista_valores.reverse()
# Volver a agregar el primer valor original a la lista:
lista_valores = [Terremotos_por_año.values[0]] + lista_valores
# Hacer una suma acumulativa para deshacer la diferenciación:
nueva_lista_valores = pd.Series(lista_valores).cumsum()
# Graficar la lista recién obtenida:
plt.plot(range(1966, 2025), nueva_lista_valores)
plt.ylabel('Número de terremotos')
# Gráfico del modelo AR(3). Pronóstico de orden 3:
plt.show()

El gráfico muestra que el modelo AR(3) no ha capturado nada: Realiza un pronóstico de línea plana.
Los primeros valores son datos reales y los últimos diez pasos son datos pronosticados. Desafortunadamente, se puede observar que el modelo no ha capturado nada interesante: ¡Solo es una línea plana! Alto, el trabajo aún no ha terminado, ya que se debe probar con un orden mayor, tal vez de , para ver si algo mejora.
Simplemente se debe cambiar el orden en la primera línea para obtener un gráfico diferente (se obtiene un pronóstico muy diferente al de la gráfica previa):
from statsmodels.regression.linear_model import yule_walker
# Realizar un pronóstico con los coeficientes estimados del modelo AR:
coeficientes, sigma = yule_walker(datos_diferenciados, order = 20)
# Hacer una lista de valores diferenciados:
lista_valores = list(datos_diferenciados)
# Invertir la lista para que el orden corresponda con el orden de los coeficientes:
lista_valores.reverse()
# Definir el número de años para predecir:
numero_pasos = 10
Atención: De nuevo, cuantos más pasos adelante se deseen pronosticar, más difícil se vuelve (es probable que el error aumente con la cantidad de pasos).
# Predecir para cada año:
for i in range(numero_pasos):
# Calcular el nuevo valor como:
# La suma de los valores rezagados.
# Multiplicada por el coeficiente correspondiente.
nuevo_valor = 0
for j in range(len(coeficientes)):
nuevo_valor += coeficientes[j] * lista_valores[j]
# Insertar el nuevo valor al principio de la lista:
lista_valores.insert(0, nuevo_valor)
# Rehacer la lista de valores al revés para mantener el orden del tiempo:
lista_valores.reverse()
# Volver a agregar el primer valor original a la lista:
lista_valores = [Terremotos_por_año.values[0]] + lista_valores
# Hacer una suma acumulativa para deshacer la diferenciación:
nueva_lista_valores = pd.Series(lista_valores).cumsum()
# Graficar la lista recién obtenida:
plt.plot(range(1966, 2025), nueva_lista_valores)
plt.ylabel('Número de terremotos')
# Gráfico del modelo AR(20). Pronóstico de orden 20:
plt.show()

El modelo parece estar aprendiendo algo mucho más interesante cuando se agrega un orden igual a : Ha capturado alguna variación.
Aunque esto parece encajar bien con los datos visualmente, aún se necesita verificar si el modelo es correcto: ¿Pronosticó algo cercano a la realidad?
Para realizar esta tarea, se utilizarán algunas estrategias y métricas comúnes en el análisis de series temporales, que serán aplicadas a este pronóstico con su respectiva descripción de manera detallada.
Evaluación y ajuste del método de división: Entrenamiento-prueba
En este caso, se aplicará un método de división: Entrenamiento-prueba. Así pues, se cortarán los últimos años del conjunto de datos y se utilizarán como el conjunto de prueba. Esto permite ajustar el modelo utilizando el resto de los datos (el conjunto de entrenamiento). Una vez que se haya ajustado el modelo en el conjunto de entrenamiento, se procede a calcular el error entre el conjunto de prueba y la predicción. El código que se muestra a continuación hace precisamente todo lo antes mencionado:
from sklearn.metrics import r2_score
# Ajustar el modelo en un conjunto de entrenamiento y evaluarlo en un conjunto de prueba:
entrenamiento = list(datos_diferenciados)[:-10]
prueba = list(Terremotos_por_año)[-10:]
coeficientes, sigma = yule_walker(entrenamiento, order = 3)
# Hacer una lista de valores diferenciados
lista_valores = list(entrenamiento)
# Invertir la lista para que el orden corresponda con el orden de los coeficientes:
lista_valores.reverse()
# Definir el número de años para predecir:
numero_pasos = 10
# Predecir para cada año:
for i in range(numero_pasos):
# Calcular el nuevo valor como:
# La suma de los valores rezagados.
# Multiplicada por el coeficiente correspondiente.
nuevo_valor = 0
for j in range(len(coeficientes)):
nuevo_valor += coeficientes[j] * lista_valores[j]
# Insertar el nuevo valor al principio de la lista:
lista_valores.insert(0, nuevo_valor)
# Rehacer la lista de valores al revés para mantener el orden del tiempo:
lista_valores.reverse()
# Volver a agregar el primer valor original a la lista:
lista_valores = [Terremotos_por_año.values[0]] + lista_valores
# Hacer una suma acumulativa para deshacer la diferenciación:
nueva_lista_valores = pd.Series(lista_valores).cumsum()
# Graficar la lista recién obtenida:
validacion = pd.DataFrame(
{
'Original': Terremotos_por_año.reset_index(drop = True),
'Predicción': nueva_lista_valores
}
)
print('Prueba R2:', r2_score(validacion.iloc[-10:, 0], validacion.iloc[-10:, 1]))
# Graficar la lista recién obtenida
plt.plot(range(1966, 2015), validacion['Original'])
plt.plot(range(1966, 2015), validacion['Predicción'])
plt.legend(validacion.columns)
plt.ylabel('Número de terremotos')
# Gráfico de pronóstico en el conjunto de prueba para el modelo AR con orden 3:
plt.show()
Prueba R2: -0.040346700807336155

Desafortunadamente, el modelo con orden 3 es bastante malo. Tan malo que el es negativo (). Puede ver en el gráfico que el modelo sufre de un ajuste insuficiente (underfitting): No capturó nada y predice solo un valor promedio en el futuro. Lo cual confirma lo que se observó antes con el orden .
En el ejemplo anterior, se ha aplicado un orden para ver si eso daría un mejor resultado. Sin embargo, la elección del orden es bastante aleatoria. Para encontrar un orden que funcione bien, se puede aplicar una búsqueda en cuadrícula.
Una búsqueda en cuadrícula consiste en hacer una evaluación del modelo para cada valor de un hiperparámetro. Los hiperparámetros son parámetros que no son estimados por el modelo sino elegidos por el modelador. El orden del modelo es un ejemplo de esto. Otros modelos a menudo tienen más hiperparámetros, lo que hace que elegir hiperparámetros sea una decisión no trivial.
Una búsqueda de cuadrícula para un parámetro es muy simple de codificar: Simplemente se ajusta el modelo para cada valor posible del hiperparámetro y se selecciona el de mejor rendimiento. Se puede usar el ejemplo del siguiente código:
# Aplicar una búsqueda en cuadrícula para encontrar el orden que da la mejor puntuación R2 en los datos de prueba:
def evaluar(orden):
entrenamiento = list(datos_diferenciados)[:-10]
prueba = list(Terremotos_por_año)[-10:]
coeficientes, sigma = yule_walker(entrenamiento, order = orden)
# Hacer una lista de valores diferenciados
lista_valores = list(entrenamiento)
# Invertir la lista para que el orden corresponda con el orden de los coeficientes:
lista_valores.reverse()
# Definir el número de años para predecir:
numero_pasos = 10
# Predecir para cada año:
for i in range(numero_pasos):
# Calcular el nuevo valor como:
# La suma de los valores rezagados.
# Multiplicada por el coeficiente correspondiente.
nuevo_valor = 0
for j in range(len(coeficientes)):
nuevo_valor += coeficientes[j] * lista_valores[j]
# Insertar el nuevo valor al principio de la lista:
lista_valores.insert(0, nuevo_valor)
# Rehacer la lista de valores al revés para mantener el orden del tiempo:
lista_valores.reverse()
# Volver a agregar el primer valor original a la lista:
lista_valores = [Terremotos_por_año.values[0]] + lista_valores
# Hacer una suma acumulativa para deshacer la diferenciación:
nueva_lista_valores = pd.Series(lista_valores).cumsum()
# Graficar la lista recién obtenida:
validacion = pd.DataFrame(
{
'Original': Terremotos_por_año.reset_index(drop = True),
'Predicción': nueva_lista_valores
}
)
return r2_score(validacion.iloc[-10:, 0], validacion.iloc[-10:, 1])
# Ajustar y evaluar el modelo para cada orden entre 1 y 30:
ordenes = []
puntajes_r2 = []
for orden in range(1, 31):
ordenes.append(orden)
puntajes_r2.append(evaluar(orden))
# Crear un marco de datos de resultados
resultados =pd.DataFrame(
{
'Orden': ordenes,
'Puntaje': puntajes_r2
}
)
# Mostrar el orden con la mejor puntuación R2:
resultados[resultados['Puntaje'] == resultados.max()['Puntaje']]
| Orden | Puntaje | |
|---|---|---|
| 18 | 19 | 0.133872 |
El código da el puntaje más alto para el orden , con una puntuación de . Lo antes mencionado significa que el modelo AR(19) explica alrededor del de la variación de los datos de prueba.
Se puede reutilizar el siguiente código para generar un gráfico con el pronóstico usando el orden (simplemente se ha cambiado el orden en la línea que ajusta los coeficientes de Yule-Walker):
from sklearn.metrics import r2_score
# Ajustar el modelo en un conjunto de entrenamiento y evaluarlo en un conjunto de prueba:
entrenamiento = list(datos_diferenciados)[:-10]
prueba = list(Terremotos_por_año)[-10:]
coeficientes, sigma = yule_walker(entrenamiento, order = 19)
# Hacer una lista de valores diferenciados
lista_valores = list(entrenamiento)
# Invertir la lista para que el orden corresponda con el orden de los coeficientes:
lista_valores.reverse()
# Definir el número de años para predecir:
numero_pasos = 10
# Predecir para cada año:
for i in range(numero_pasos):
# Calcular el nuevo valor como:
# La suma de los valores rezagados.
# Multiplicada por el coeficiente correspondiente.
nuevo_valor = 0
for j in range(len(coeficientes)):
nuevo_valor += coeficientes[j] * lista_valores[j]
# Insertar el nuevo valor al principio de la lista:
lista_valores.insert(0, nuevo_valor)
# Rehacer la lista de valores al revés para mantener el orden del tiempo:
lista_valores.reverse()
# Volver a agregar el primer valor original a la lista:
lista_valores = [Terremotos_por_año.values[0]] + lista_valores
# Hacer una suma acumulativa para deshacer la diferenciación:
nueva_lista_valores = pd.Series(lista_valores).cumsum()
# Graficar la lista recién obtenida:
validacion = pd.DataFrame(
{
'Original': Terremotos_por_año.reset_index(drop = True),
'Predicción': nueva_lista_valores
}
)
print('Prueba R2:', r2_score(validacion.iloc[-10:, 0], validacion.iloc[-10:, 1]))
# Graficar la lista recién obtenida
plt.plot(range(1966, 2015), validacion['Original'])
plt.plot(range(1966, 2015), validacion['Predicción'])
plt.legend(validacion.columns)
plt.ylabel('Número de terremotos')
# Gráfico de pronóstico en el conjunto de prueba para el modelo AR con orden 19:
plt.show()
Prueba R2: 0.1338715328132314

Este código muestra gráfico para el modelo con orden . Así pues, se puede observar que, aunque no es perfecto, el modelo se ajusta un poco mejor que el modelo con orden .
El modelo AR es uno de los componentes básicos de las series temporales univariadas. Resulta importante mencionar que se puede usar como modelo independiente solo en casos muy raros y específicos.
En este ejemplo de la vida real sobre la predicción de terremotos, la puntuación de no es muy buena: Seguramente se puede hacer mucho mejor si se incluyen otros componentes básicos de series temporales univariadas.
Conclusiones clave
- El modelo AR predice el futuro de una variable aprovechando las correlaciones entre los valores pasados y presentes de una variable.
- La autocorrelación es la correlación entre una serie de tiempo y sus valores anteriores.
- La autocorrelación parcial es una autocorrelación condicionada a retrasos anteriores: Evita las correlaciones de conteo doble.
- El número de retrasos que se incluirán en el modelo AR puede basarse en la teoría (gráficos ACF y PACF) o puede determinarse mediante una búsqueda en cuadrícula.
- Una búsqueda en cuadrícula consiste en hacer una evaluación del modelo para cada valor de los hiperparámetros de un modelo. Este es un método de optimización para la elección de hiperparámetros.
- Los hiperparámetros son diferentes de los coeficientes del modelo. Los coeficientes del modelo son optimizados por un modelo, mientras que el modelador elige los hiperparámetros. Sin embargo, el modelo puede usar técnicas de optimización como una búsqueda en cuadrícula para encontrar los mejores hiperparámetros.
- Las ecuaciones de Yule-Walker se utilizan para ajustar el modelo AR. Ajustar el modelo significa encontrar los coeficientes del modelo.
popular post

El modelo AR de series temporales univariadas
Resumen: En esta entrada, descubrirá el modelo AR: El modelo autorregresivo.
Leer más
Evaluación de modelos para pronosticar
Resumen: Al desarrollar modelos de aprendizaje automático, generalmente se comparan varios modelos durante la fase de construcción.
Leer más
Modelos para pronosticar
Resumen: El pronóstico, traducido groseramente como la tarea de predecir el futuro, ha estado presente en la sociedad humana durante siglos.
Leer más